Support Vector Regression-based Model to Analyze Prognosis of Infants with Congenital Muscular Torticollis
Article information
Abstract
Objectives
Congenital muscular torticollis, a common disorder that refers to the shortening of the sternocleidomastoid in infants, is sensitive to correction through physical therapy when treated early. If physical therapy is unsuccessful, surgery is required. In this study, we developed a support vector regression model for congenital muscular torticollis to investigate the prognosis of the physical therapy treatent in infants.
Methods
Fifty-nine infants with congenital muscular torticollis received physical therapy until the degree of neck tilt was less than 5°. After treatment, the mass diameter was reevaluated. Based on the data, a support vector regression model was applied to predict the prognoses.
Results
10-, 20-, and 50-fold cross-tabulation analyses for the proposed model were conducted based on support vector regression and conventional multi-regression method based on least squares. The proposed methodbased on support vector regression was robust and enabled the effective analysis of even a small amount of data containing outliers.
Conclusions
The developed support vector regression model is an effective prognostic tool for infants with congenital muscular torticollis who receive physical therapy.
I. Introduction
Torticollis is a condition that head is tilted to one side, and chin is tilted to opposite side. Congenital muscular torticollis (CMT) is a common disorder which is caused by short-ening of the sternocleidomastoid for infants [1-4]. In general, CMT is occurred at birth or up to two months old, and it reacts sensitively to physical therapies. If the condition is not recovered by early treatment, the infants with CMT will be unable to move head properly, and operative treatments [5] or Botox injection treatments [6,7] will be needed to correct the shortened muscle. Therefore early diagnosis and treatment are extremely important for CMT [2,3]. Mostly, CMT is detected in early stage by parents, and physical therapies are performed steadily. However procedure of physical therapy is not systematically organized, and researches for the prognosis of CMT according to treatments are still inadequate [8,9].
Recently research of prediction model based on conventional multiple regression to analyze the prognosis of CMT according to treatments has been proposed [9]. However the performance of the conventional statistical models depends on quality and amount of the training data, and the shapes of the models that are constructed by conventional methods are extremely influenced by outliers, because the conventional methods are based on empirical risk minimization (ERM) [10,11]. Therefore, in data mining, it is recommended to perform regression after eliminating low quality data such as outliers from large amount of training data as possible [11,12]. Nevertheless to collect large amount of high quality data through observation and experience is limited and difficult, especially, for clinical data. Moreover the outliers in clinical data are recognized as objects with major information. Thus a method which is robust and possible to analyze effectively clinical data is needed.
Based on the needs, in this study, we propose support vector regression (SVR)-based method, which has degree of neck tilt, face symmetry, initial mass diameter, age, and treatment duration as the independent variables, to predict the change of mass diameter after treatments, and to overcome the drawbacks of conventional methods. SVR is not based on ERM but based on structural risk minimization (SRM), and SVR performs data analysis in feature space of high dimension which is mapped by kernel function such as polynomial, Gaussian radial basis function (RBF), exponential radial basis function, splines, and etc [13-16]. Therefore SVR is able to minimize generalization error effectively, and minimize the influence of amount and quality of the collected data [10]. We show the effectiveness of the proposed SVR-based prediction model for CMT through experiments based on data with fifty nine infants of CMT and discuss it.
II. Methods
1. Object of study and data collection
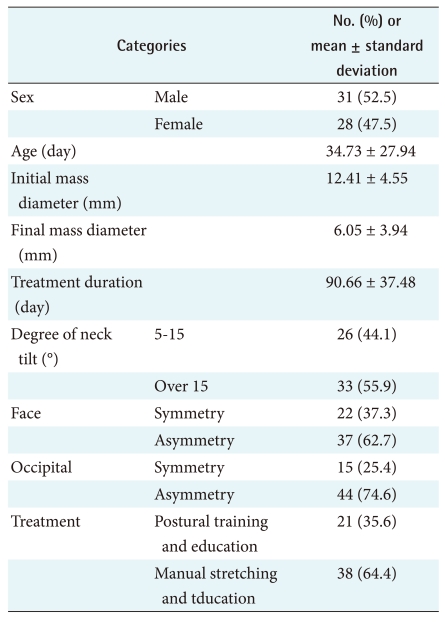
In this study, data of fifty nine infants with CMT who visited D medical center in Daegu is collected from April 2003 to December 2008. During the same period, others who have neurologic problems, congenital malformations of cervical vertebra, and ocular torticollis were not included in this study. Data is categorized according to sex, age, initial and final mass diameter, treatment duration, degree of neck tilt, face symmetry, occipital symmetry, and treatment methods that are summarized in Table 1.
The physical therapies are performed twice a week by three people who have more than five years experience for CMT and the therapies are finished when the degree of neck tilt of infants with CMT is less than five degree, and asymmetric form is disappeared. Duration of the physical therapies and change of the mass diameter after treatment are 90.66 ± 37.48 mm and 6.36 ± 2.56 mm respectively.
2. SVR-based prediction model
Regression is a statistical method which is widely used to predict and analyze the relationship of data between a dependent variable and one or more independent variables. Many kinds of regression methods have been proposed and these can be classified as simple regression and multiple regressions according to the number of independent variables. Regression model can be represented as a function f which is related dependent variable Y.

where X is independent variables and β is unknown parameters.
To estimate appropriate regression model, it is recommended to perform regression with large amount data after eliminating outliers by using standardized residual or studentized residual, because the conventional regression models are extremely influenced by amount and quality of data as shown in Figure 1.
However to collect large amount with high quality of data is limited, especially, in clinical cases, and outlier is recognized as important object which contains useful information. Therefore, in this study, SVR-based method, which is possible to analyze small amount of clinical data with outliers effectively, is proposed to overcome the drawbacks of the conventional statistical analysis methods.
SVR is constructing regression model by minimizing generalization error based on SRM while other statistical methods are based on ERM [14]. Moreover SVR performs data analysis in high dimensional feature space which is mapped by kernel function such as polynomial, RBF, and etc. Therefore SVR is possible to deal with small amount of data with outliers.
Suppose the given training data {(xi, yi),…,(xN, yN)}⊂χ × R, where N denotes number of data, x, y denote input and output vector respectively, and χ denotes input data space. The goal of SVR is to find a function f that has minimum ω less than ε deviation from the target yi.

where <·,·> denotes the dot product in χ.
Convex optimization problem to find minimum ω can be rewritten as follows.

However, from the Equation (3), it is impossible to analyze the training data that exists out of the bound ε. Therefore, to overcome it, slack variables ξi, ξi* are applied, then Equation (3) can be rewritten as follows.

In here, regularization constant C > 0 controls model complexity by determining how much of error will be allowed for training data that is out of the bound ε.
By applying Lagrange function to solve Equation (4) and kernel function to map data into high dimensional space, it can be rewritten as Equation (5) and (6) [13-15].
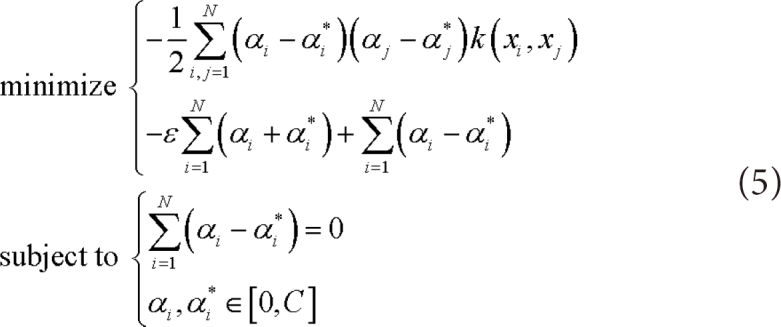
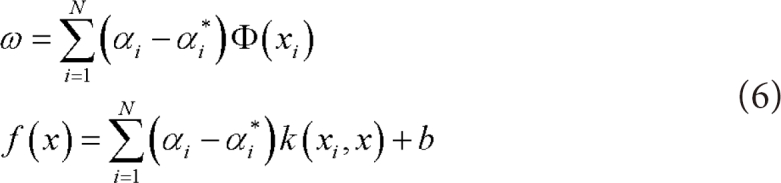
where k (x, x') := <Φ (x), Φ (x')> and Φ denote mapping function and k denotes kernel function.
Typical kernel functions and their parameters are summarized in Table 2.
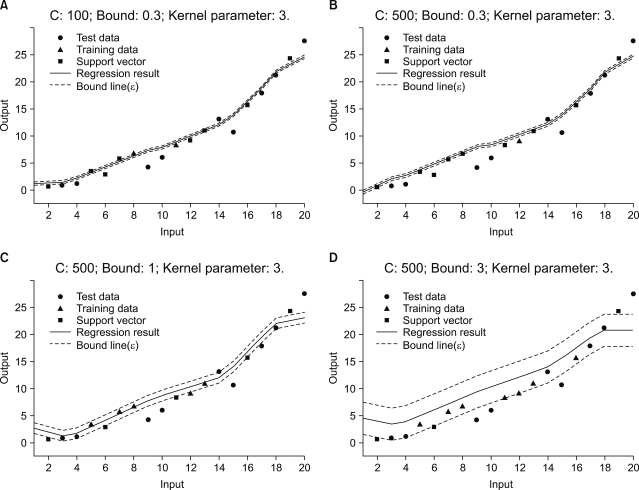
The performance of SVR is closely related to SVR parameters and kernel function. The examples for SVR parameters (C: regularization constant, ε: error bound) are shown in Figure 2.
From Figure 2A and 2B, SVR parameter C is related to the complexity of model. That is, the complexity of regression model is increased as C is increased. Therefore, we could compose a model which has minimum training error by selecting higher value of C. However, testing error will be increased with higher value of C, because of overfitting problem.
Moreover Figure 2C and 2D show the influence of SVR parameter ε. ε controls model complexity similar with C. The difference of C and ε is that C controls complexity by adjusting the error sensitivity of training data, and ε controls complexity by adjusting the number of support vectors. As shown in Figure 2C and 2D, the number of support vector is decreased and the regression model is simplified as ε is increased.
Therefore, to select optimal parameter is important to construct proper regression model based on SVR. In this study, we have tested on several conditions (C: 500 and 1,000; ε : 0.001 and 0.005; and Gaussian RBF kernel parameter: 2 and 4). According to the condition, we have constructed SVR prediction model to analyze the change of mass diameter on CMT.
To analyze the change of mass diameter on CMT, we have collected data of fifty nine infants with CMT. From the CMT data, we select independent variables based on t-test and Pearson's correlation coefficient. After selecting independent variables, we constructed SVR prediction model using Gaussian RBF kernel. The algorithm of this study is summarized as follows.
Step 1] Collect data of infants with CMT.
Step 2] Select independent variables using t-test and Pearson's correlation coefficient method.
Step 3] Construct SVR prediction model according to SVR parameters.
Step 4] Evaluate the performance of SVR model according to parameters based on root mean square error (RMSE).
The architecture of SVR is shown in Figure 3.
III. Results
The change of diameter is used as dependent variable, and t-test, Pearson's correlation coefficient methods according to data types have been used to select optimal independent variables. The results of t-test and Pearson's correlation coefficient methods are summarized in Tables 3 and 4.
In general, p-value is set as under 0.05. However the data set used in this study is not large amount of data set without outliers. Therefore we have set the p-value as 0.1 to consider many cases as possible. Based on the p-value, degree of neck tilt, face symmetry, initial mass diameter, age and treatment duration have been selected as independent variables which have relationship with change of mass diameter from the result of statistical hypothesis tests shown in Tables 3 and 4.
Using the selected independent variables, we have constructed SVR regression model with Gaussian RBF kernel according to parameters. To show the effectiveness of the proposed SVR model, we demonstrated 10-, 20-, and 50-fold cross tabulation analysis (training 15 [25%] and test 44 [75%]). Moreover RMSEs between the proposed SVR-based method and conventional multi-regression method using least squares have been compared. The results are summarized in Table 5.
Table 5 shows RMSE results of the proposed SVR prediction model and conventional multi-regression model according to 10-, 20-, and 50-fold cross tabulation conditions. From Table 5, the proposed method showed 2.66 ± 0.07, 2.66 ± 0.06, and 2.69 ± 0.03 results according to cross tabulation conditions (10-, 20-, and 50-fold). Moreover the conventional method showed 3.31 ± 1.01, 3.36 ± 0.73, and 3.22 ± 0.39 results according to cross tabulation conditions (10-, 20-, and 50-fold).
Based on the overall comparison results, the proposed method provides more robust and steady results than the conventional method. Especially, from the last results of 10-fold, standard deviations of the proposed method and conventional multi-regression method are 0.07 and 1.01 respectively. That is, the proposed SVR method provides proper results with minimizing influence of amount and quality of the collected data.
Through the experiment, it is shown that the proposed SVR model precisely predicts the change of diameter by reducing the effects of amount of data and quality, while the result of the conventional regression method depends on amount and the quality of data.
IV. Discussion
Congenital muscular torticollis is a common disorder that the sternoclavicularmastoid is shortened by fibrosis for infants. Most of all infants with CMT are discovered within two weeks and get physical therapies to treat CMT. However the researches to analyze the prognosis of the physical therapies for CMT are inadequate. Therefore, in this study, we proposed a SVR-based method to analysis the prognosis of who get the physical therapies to treat CMT, and overcome the drawbacks of conventional statistical analysis methods.
From the results in section III, we have confirmed that the treatment methods are not statistically significant as mentioned in reference [17]. Moreover we have found out that degree of neck tilt, face, initial mass diameter, age, and treatment duration are statistically significant under 0.1 of p-value. Based on the selected independent variables, we have shown that the proposed SVR-based method provides steady and appropriate results from 10-, 20-, and 50-fold cross tabulation analysis according to SVR parameters, while the conventional method does not.
In medical informatics which use the clinical data, there is a limitation to compose robust diagnosis and prediction systems based on lots of data with high quality because the history of electronic medical record (EMR) system is not long enough to build up large amount of various clinical data in domestic case. Therefore diagnosis and prediction systems based on the conventional statistical methods, which depend on amount and quality of data, have drawbacks. However SVR method, which is based on SRM, could provide robust results as shown in section III. Thus, in medical informatics, we expect that SVR-based system is possible to apply to various other clinical cases to compose diagnosis and prediction systems.
However the selection of parameters is important because the parameters are directly related to control the complexity of regression model. That is, if the constructed model is tightly fitted to training data by tuning the parameters, then the generalization error will be increased. Oppositely, if the constructed model is too simple, then the model could not represent the characteristic of data. Various researches have been proposed to select the optimal parameters based on given data and expert knowledge, especially, in engineering application. Nonetheless, the algorithms are mostly based on the exhaustive searching method such as grid searching. Therefore the computational complexity is increased as the complexity of given feature set is increased. In the case of clinical data, the feature set is more complex than the feature set of other applications. To overcome the limitation, the researches for feature reduction and optimal parameters selection are required. Thus we remain these issues as further studies to be solved.
Acknowledgements
This research was supported by the grant No. RTI04-01-01 from the Regional Technology Innovation Program of Ministry of Knowledge Economy (MKE).
The authors are very grateful to the anonymous reviewers for the critical and constructive comments and suggestions to improve the presentation and quality of this paper.
Notes
No potential conflict of interest relevant to this article was reported.