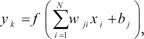I. Introduction
Diabetes is one of the most common non-communicable disease (NCDs) that has significantly contributed to increased mortality in patients. It is assuredly one of the most challenging health problems in the 21st century that evidently is epidemic in a large number of developing countries [
1]. About 135 million people have been estimated to have diabetes, and it is expected to increase to about 300 million by the year 2025 [
2].
Besides diabetes, the condition of impaired glucose tolerance (IGT) or pre-diabetes, with elevated blood glucose levels that increase the risk of developing diabetes, heart disease, and stroke, is also a major public health problem [
1]. People with diabetes are at risk of severe and fatal complications [
3]. Cardiovascular disease, stroke, retinopathy and blindness, peripheral neuropathy, end-stage renal disease, and mutilation (amputation) are the most serious complications of diabetes [
4]. It has been noted in recent studies that by changes in lifestyle or pharmacotherapy, diabetes can be avoided by pre-diabetic persons [
5]. Therefore, early screening and diagnosis of diabetes mellitus plays an important role in effective prevention strategies [
6]. Moreover, because of the seriousness of diabetes and its complications, providing an efficient and accurate model to predict persons prone to diabetes, especially based on demographic characteristics, is an important issue that should be investigated.
To achieve this purpose, it is possible to identify people who are at risk for the development of diabetes based on common risk factors, such as body mass index (BMI) and family history of diabetes, through a number of predictive models, such as logistic regression [
7]. Ideally, it would be important to amend the predictive power of the models predicting diabetes via learning theory and data mining techniques for classification that require no distributional assumptions. Classical techniques, such as logistic regression (LR) and Fisher linear discriminant analysis (LDA), have been widely used for classification of various problems, especially medical ones where the dependent variable is dichotomous [
8].
Recently, the positive performance of data mining methods, with classifiers like neural networks (NN), support vector machines (SVM), fuzzy c-mean (FCM), and random forests (RF), has led to considerable research interest in their application to prediction and classification problems [
2,
7-
9].
Research comparing the accuracy of traditional classifiers and computer intensive data mining methods has been steadily increasing. Three data mining method (NN, SVM, and decision tree) were assessed and compared by Kim et al. [
10] in a study with LR for mortality prediction. Maroco et al. [
8] evaluated various data mining and traditional classifiers (LDA, LR, NN, SVM, classification tree, and RF) for Alzheimer disease. Son et al. [
11] compared various kernel functions in the SVM technique for predicting medication adherence in heart failure patients. In another study conducted by Lee et al. [
12], the performance of SVM was evaluated and compared with LR for the classification of chronic disease. In a study conducted by Lehmann et al. [
13], the performance of four classification methods (RF, SVM, NN, and LDA) were compared for recognition of Alzheimer disease. Hachesu et al. [
14] evaluated and compared the performance of three algorithms, namely, decision tree, SVM, and NN, for the classification of coronary artery disease. However, there has been relatively little research related to the performance of data mining methods and comparison of them in diabetes prediction. Yu et al. [
9] compared SVM and LR for the classification of undiagnosed diabetes or pre-diabetes vs. no diabetes. Priya and Aruna [
15] compared NN and SVM for the diagnosis of diabetic retinopathy.
Although, some authors maintain that classification based on data mining techniques has higher accuracy and lower error rates than the traditional methods (LDA and LR), this excellence is not apparent with all data sets [
16-
19]. The results of various studies are inconsistent regarding classification accuracy of data mining classifiers as compared to traditional, less computer demanding methods, and there is disagreement regarding the stability of the findings [
16,
20]. To our knowledge, there has not been a study comparing various data mining classifiers like NN, FCM, RF, and SVM with traditional classifiers for predicting diabetes.
The aim of this study was to provide a comprehensive comparison of six methods (two classic methods and four commonly used data mining methods), namely, LR, LDA, NN, FCM, RF, and SVM, and apply these methods to distinguish people with either undiagnosed diabetes or pre-diabetes from people without these conditions in the Iranian population.
II. Methods
1. Data Source
This study used a data set obtained from the Iranian national NCDs risk factors surveillance through a cross-sectional study which was conducted in 2005-2009 to assess the prevalence of major NCDs risk factors [
21].
A two-stage cluster sampling method was used for data collection. As mentioned in [
21], the data collection included three steps:
Step 1: collecting questionnaire-based information about health history and behavioral information;
Step 2: using standardized physical measurements to collect physical and physiological data;
Step 3: taking blood samples for biochemical measurement and laboratory examinations of lipids and glucose status that were performed by trained personnel.
The total sample size was 6,500. Participants were diagnosed with diabetes if they had a measured fasting blood sugar (FBS) Ōēź126 mg/dL, and those with FBS of 110 to 125 mg/dL were considered to have undiagnosed diabetes or pre-diabetes (as IGT). Participants with FBS <110 mg/dL were considered not to have diabetes. To create a dichotomous classification, the diabetic and pre-diabetic subjects were classified as a single group and were compared with those without diabetes.
We selected 10 risk factors that are commonly associated with diabetes, including age, gender, BMI, waist circumference, smoking, job, hypertension, residential region (rural/urban), physical activity, and family history of diabetes.
2. Data Pre-processing and Dealing with Missing Values
Pre-processing of the data set was done in two steps. First, fields with spelling errors, additional tokens, other irregularities and irrelevancies, such as outliers were removed or corrected. Second, because of the missing completely at random (MCAR) mechanism for missingness based on Little MCAR test [
22] (
p = 0.561), persons with at least one missing variable were removed from analysis.
Table 1 shows the demographic and clinical characteristics of the participants.
3. Data Mining Algorithms
1) Neural networks
The NNs method is a flexible mathematical conformation for information processing which is well suited for forecasting, pattern recognition, and classification problems. NNs include multiple input nodes and weighted interconnections [
14]. One of the most used NNs is the multilayer perceptron (MLP), in which its neurons apply a nonlinear activation function to calculate their outputs. The activation function includes a sigmoid function (
f(
x) = 1 / (1 + exp(
-x))) in the hidden layer and a linear function (
fj(
x) =
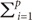 wijxi
wijxi, where
xi's are predictor variables and
wij's are input weights) in the output layer. The functional form of the MLP can be written as
where
xi is the
i-th nodal value in the previous layer,
yj is the
j-th nodal value in the present layer,
bj is the bias of the
j-th node in the present layer,
wji is a weight connecting
xi and
yj,
N is the number of nodes in the previous layer, and
f is the activation function in the present layer [
23].
2) Support vector machines
The SVM is a supervised machine learning technique which has wide application in regression and classification problems. The SVM algorithm carries out a classification by mapping a vector of predictors into a higher dimensional plane via maximization of the margin between two data classes [
23]. High discriminative power is achieved by using either linear or non-linear kernel functions to alter the input space into a multidimensional space [
9].
In the binary classification mode, the equation of the hyperplane segregating two groups, say {-1, +1} in a higher-dimension feature space is given by the relation
y(
t)=╬Ż
 wi╬”i
wi╬”i +
b = o, where {
╬”i(
x)}

denotes features,
b and {
wi}

denote coefficients that have to be estimated from the data, and {(
xi,
yi)}
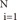
are a set of samples where
yiŌłł{+1, -1}.
In summary, the goal of SVM can be regarded as the solution of the following quadratic optimization problem:
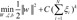
subject to
yi(
wT.╬”(
wi)+
b)Ōēź1-╬Š
i, where ╬Š
iŌēź
0,
i=
1, ..., n, where the training data are mapped to a higher dimensional space by the function
╬”, and
C is a user-defined penalty parameter on the training error that controls the trade-off between classification errors and the complexity of the model. Therefore, the decision function (predictor) is
f(
x)=sign(
wT╬”(
x)+
b), where x is any testing vector [
11].
In addition, to derive the optimal hyperplane for not linearly separated data, several solutions called kernel functions have been proposed and adopted for SVM. A kernel function is written as K(xi, xj)=╬”(xi)T╬”(xj), and the most widely used four kernel functions are the linear (K(xi, xj)=xiTxj); radial basis function (RBF) (K(xi, xj) = exp(-╬│Ōłźxi-xjŌłź2), where ╬│ is the kernel parameter); polynomial (K(xi, xj) = (xiTxj+1)d, d > 0 is the degree of the polynomial kernel); and sigmoid (K(xi, xj) = tanh(wiTxj+1)).
3) Random forests
RF is a new "ensemble learning" method in classification which is designed to produce accurate predictions without over fitting the data [
8]. This method constructs a series of unpruned classification trees using random bootstrap samples of the original data sample. The outputs of all trees are aggregated to produce one final classification, i.e., the object belongs to a class with the majority of predictions given by the trees in the random forest [
8].
4) Fuzzy c-mean
FCM is a method of clustering in which each piece of data may belong to more than one cluster [
2] with varying degrees of membership for each cluster. The goal of this method can be regarded as minimizing of the following objective function via an iterative optimization algorithm:
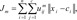
1<
m <
a, where
m is any real number greater than 1 which is called the fuzziness index and controls the fuzziness of membership of each observation,
xi is the
i-th component of
d-dimensional observed data,
uij is the degree of membership of
xi in cluster
j(
uijŌłł[0,1],
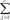 uij
uij=1 ŌłĆ
i=1,2,...,
n, ŌłĆ
j=1,2,...,
c),
cj is the
d-dimension center of the cluster, and ŌłźŌłź is any norm, such as Euclidean distance expressing the similarity between any observed data and the center of cluster [
2].
4. Implementation and Performance Criteria
To avoid overfitting due to the use of the same data for the training and testing of different classification methods, a 10-fold cross-validation strategy was used in the training data set. In this regard, the total data set was partitioned into 10 nearly equal subsets. In each of the 10 steps, 9/10 of the sample was used for training and 1/10 for testing.
In this research, all classification methods were implemented on the diabetes data set by using R packages [
24] (e1071, nnet, randomForest, glmnet, MASS and pROC) through related functions (e.g.,"cmeans", "svm", "nnet", "randomForest", "lda", and "glm"). The SVM-based model building process was carried out with RBF as kernels. Also, this study employed an MLP with one hidden layer to construct the NN model for the diabetes data set. After fitting the models using the 10-fold cross-validation strategy, predicted values were obtained to evaluate the methods' performance.
To compare the discriminative powers of the six models, receiver operating characteristic (ROC) curves were generated based on the predicted outcome and true outcome, and the area under the curves (AUCs) for the data sets were calculated.
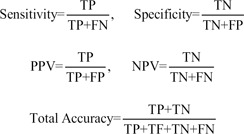
Sensitivity, specificity, positive predictive value (PPV), negative predictive value (NPV), and total accuracy were calculated based on the following formulas:
where TP, FP, TN, and FN represent the number of true positives, false positives, true negatives, and false negatives, respectively [
9].
In addition, to find the optimal cut-off point value for calculation of predictive performance in LR, several points were examined, and 0.1 was obtained.
III. Results
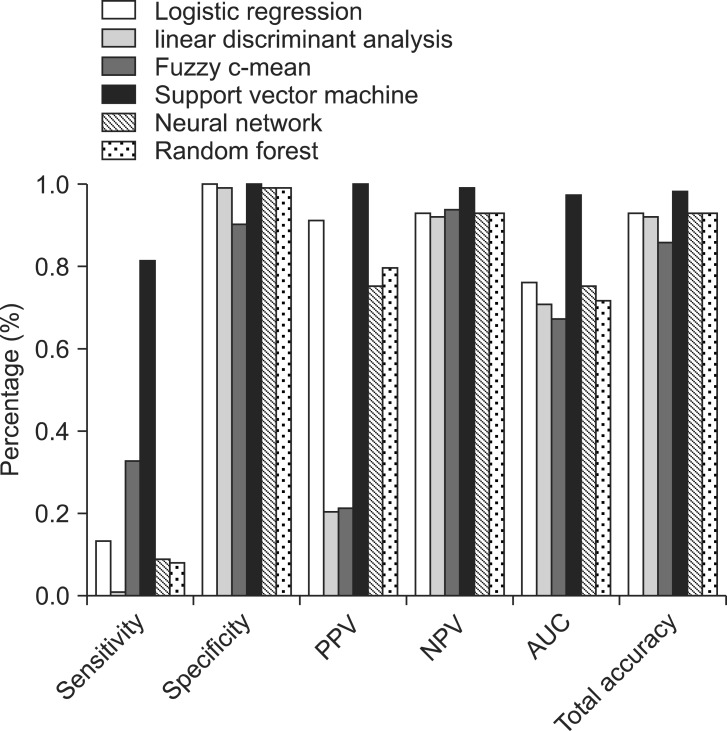
The performance of the six classifiers was evaluated in terms of their discriminative accuracy by AUC, sensitivity (the proportion of persons that have diabetes and were correctly diagnosed), specificity (the proportion of persons that did not have diabetes and were correctly diagnosed), PPV, NPV, and total accuracy (
Table 2;
Figure 1) from the 10-fold cross validation strategy. A graphical comparison of six quantities is shown in
Figure 1 to evaluate the performance of the models.
As seen in
Table 2, almost all the algorithms generate high specificity (more than 90%). However, the sensitivity values of the classical methods (LR, 13.3%; LDA, 0.6%), NN (8%) and RF (8%) were very low, and the sensitivity of FCM (33%) was relatively low. In addition, the highest sensitivity in our experiments was obtained with SVM (82%).
Although, the PPV of the LDA (20%) and FCM was relatively low in comparison with the other four methods (SVM, 100%; LR, 91.4%; RF, 79.5%; and NN, 75%), the NPV performance of these two (92.6% for LDA and 94.4% for FCM) is as good as that of the other four technique (SVM, 99.1%; LR, 93.5%; RF, 93.2%; and NN, 93.1%).
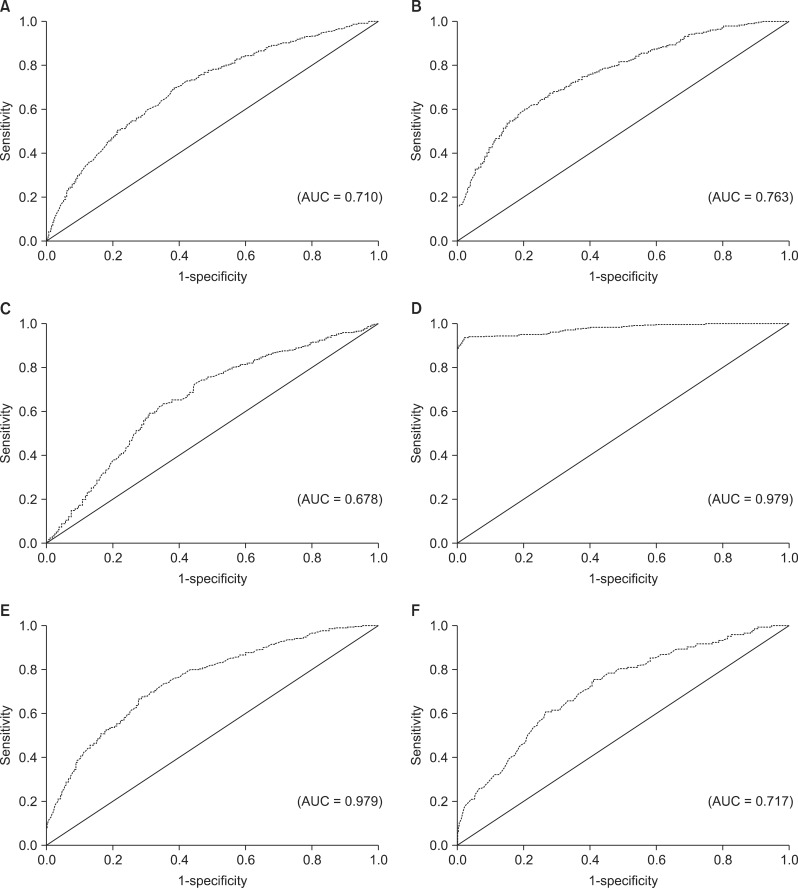
The overall discriminative ability of classification schemes is represented by their AUC values, which are 97.9% for SVM with RBF kernel, 76.3% for LR, 75.1% for NN, 71.7% for RF, and 67.8% for FCM (
Table 2;
Figure 2). Furthermore, all techniques produced a total accuracy of more than 85%. The highest total accuracy was achieved by SVM.
Thus, the SVM approach appears to perform better than the traditional models and the other three data mining methods.
IV. Discussion
It is clear from the sensitivity, specificity, and AUC values presented here that SVM has a distinct advantage over the other methods in terms of predictive capabilities, and it is more effective than LR, LDA, FCM, RF, and NN.
With the exception for FCM (0.67), in terms of AUC, the discriminant power of classification methods was appropriate for most classifiers (more than 0.7). Specificity ranged from a minimum of 0.901 (FCM) to a maximum of 1 (SVM). All the classifiers were quite efficient in predicting group membership in the group with a larger number of elements (the normal group corresponding to 93% of the sample). In terms of total accuracy, SVM outperformed all other classification methods; however, other methods also achieved high total accuracy (more than 0.85).
Judging from the sensitivity of the classification methods, prediction for the group with lower frequency (the diabetic group, 7% of the sample) was quite poor for almost all the used classifiers, with the exception of SVM, despite its high specificity and total accuracy.
The minimum sensitivity value was 0.006 (LDA), and maximum sensitivity was 0.820 (SVM, followed by 0.33 for FCM). Only one of the six tested classifiers showed a sensitivity value higher than 0.5.
Considering that having diabetes is the key prediction in this biomedical application, a classification method with higher sensitivity is desired; therefore, classification methods, such as LR, NN, FCM, RF, and LDA, are inappropriate for this type of binary classification task. However, SVM showed a good sensitivity result; hence, it is an appropriate method for classification. This finding is similar to the results of other works comparing various classification methods in other biomedical conditions [
2,
9].
In a study to compare NN and SVM for diagnosing diabetic retinopathy, Priya and Aruna [
15] reported better performance for SVM (accuracy 89.6% for NN and 97.61% for SVM). In a study comparing three data mining methods (NN, SVM, and decision tree) with LR, Kim et al. [
10] concluded that the decision tree algorithm slightly outperformed (AUC, 0.892) the other data mining techniques, followed by the artificial neural network (AUC, 0.874) and SVM (AUC, 0.876), which is in contradiction to our results.
In another study [
2] titled "Review of automated diagnosis of diabetic retinopathy" using the support vector machine achieved 99.45% for sensitivity and 100% for specificity, which is similar to our results.
Son et al. [
11] demonstrated that SVM with appropriate kernel function can be a promising tool for predicting medication adherence in heart failure patients (sensitivity, 77.6%; specificity, 81.6%; PPV, 77.8%; NPV, 77.6%; and total accuracy, 77.6%)
Lehmann et al. [
13] compared several classification methods (RF, SVM, NN, and LDA) for recognition of Alzheimer disease and found that data mining classifiers show a slight superiority compared to classical ones, whereas in our work SVM showed a high performance compare to the other methods. In their study, the sensitivity and specificity of SVM were 89% and 88%, respectively.
In a study conducted by Hachesu et al. [
14], three algorithms, namely, decision tree, SVM and NN, were compared for the classification of coronary artery disease. Their findings demonstrated that all three algorithms showed various acceptable degrees of accuracy for prediction, and the SVM was the best fit (96.4% total accuracy and 98.1% sensitivity), which is similar to our results.
Maroco et al. [
8] reported in their comparison study of data mining and traditional classifiers (LDA, LR, NN, SVM, classification tree, and RF) the highest total accuracy and specificity for SVM and the lowest sensitivity, while in the present study, SVM had the highest sensitivity. Yu et al. [
9], in a comparison between SVM and LR for the classification of undiagnosed diabetes or pre-diabetes vs. no diabetes, showed that the SVM performance based on AUC is as good as that of LR (73.2% for SVM and 73.4 for LR). In contrast, the performance of SVM in our study was better than that of LR.
In another study Lee et al. [
12] compared SVM and LR for the classification of chronic disease and showed that SVM achieved higher accuracy with a smaller number of variables than the number of variables used in LR (71.1% for LR and 97.3% for SVM), which is consistent with our results.
Some methods are only good for predicting the larger group membership (high specificity) but quite insufficient in predicting the smaller group membership (low sensitivity); therefore, selecting classification methods only based on total accuracy can be spurious [
8]. Some real-data studies have reported unbalanced efficiency for small frequency vs. large frequency groups in LR, NN, and SVM [
8,
20,
25]. However, to our knowledge, such imbalance of RF has not been published elsewhere.
Based on the six performance criteria (total accuracy, specificity, sensitivity, PPV, NPV, and AUC), the traditional classifiers (LDA and LR) appear to perform as well as the FCM, NN, and RF (the newest member of the binary classification family).
It seems that the relatively low observed prevalence of diabetes may limit the performance of some data mining methods evaluated in this study. The present unbalanced sample sizes of two groups did not limit the achievement of acceptable accuracy, specificity, and sensitivity of SVM as reported by other studies [
15,
26,
27]. Furthermore, there have been studies with fairly small samples in which new classification methods such as RF and NN have been applied with high accuracy [
8,
13,
28]. Some studies have reported equivalent or even superior performance of LR and LDA in comparison with NN, SVM, RF, and FCM [
9,
13,
20,
29,
30]. Since the performance of NN and SVM depends on tuning parameters, these parameters were optimally determined by grid search.
This study focused on the performance of six classification methods in detecting cases of diabetes and pre-diabetes in the Iranian population. Our results demonstrated that the discriminative performance of SVM models was superior to that of other commonly used methods. Therefore, it can be applied successfully for the detection of a common disease with simple clinical measurements. SVM is a nonparametric method that provides efficient solutions to classification problems without any assumption regarding the distribution of data. The SVM method is a learning machine technique in modeling nonlinearity based on minimization of structural risk which avoids finding local minimums instead of general ones because of minimizing structural risk function. Because of the convex optimality problem, SVM gives a unique solution. This is an advantage of SVM compared to other methods, such as NN, which have multiple solutions associated with local minimum and for this reason may not be robust over different samples. In addition, with appropriate choice of kernel function (e.g., RBF kernel) and related parameters, the similarity between individuals is increased. Therefore, when classifying a new subject, it is assigned to the group with the highest similarity [
31].
This work demonstrates the predictive power of the SVM with unequal sample sizes. Yu et al. [
9] performed a similar study in which they compared LR and SVM performance on diabetes data and concluded that the SVM approach performed as well as the LR model.
Generally, one cannot find a method that always is the best for the classification of different datasets.
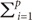 wijxi, where xi's are predictor variables and wij's are input weights) in the output layer. The functional form of the MLP can be written as
wijxi, where xi's are predictor variables and wij's are input weights) in the output layer. The functional form of the MLP can be written as wi╬”i + b = o, where {╬”i(x)}
wi╬”i + b = o, where {╬”i(x)} denotes features, b and {wi}
denotes features, b and {wi} denote coefficients that have to be estimated from the data, and {(xi, yi)}
denote coefficients that have to be estimated from the data, and {(xi, yi)}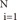 are a set of samples where yiŌłł{+1, -1}.
are a set of samples where yiŌłł{+1, -1}.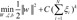 subject to yi(wT.╬”(wi)+b)Ōēź1-╬Ši, where ╬ŠiŌēź0, i=1, ..., n, where the training data are mapped to a higher dimensional space by the function ╬”, and C is a user-defined penalty parameter on the training error that controls the trade-off between classification errors and the complexity of the model. Therefore, the decision function (predictor) is f(x)=sign(wT╬”(x)+b), where x is any testing vector [11].
subject to yi(wT.╬”(wi)+b)Ōēź1-╬Ši, where ╬ŠiŌēź0, i=1, ..., n, where the training data are mapped to a higher dimensional space by the function ╬”, and C is a user-defined penalty parameter on the training error that controls the trade-off between classification errors and the complexity of the model. Therefore, the decision function (predictor) is f(x)=sign(wT╬”(x)+b), where x is any testing vector [11].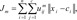 1<m <a, where m is any real number greater than 1 which is called the fuzziness index and controls the fuzziness of membership of each observation, xi is the i-th component of d-dimensional observed data, uij is the degree of membership of xi in cluster j(uijŌłł[0,1],
1<m <a, where m is any real number greater than 1 which is called the fuzziness index and controls the fuzziness of membership of each observation, xi is the i-th component of d-dimensional observed data, uij is the degree of membership of xi in cluster j(uijŌłł[0,1], 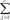 uij=1 ŌłĆi=1,2,...,n, ŌłĆj=1,2,...,c), cj is the d-dimension center of the cluster, and ŌłźŌłź is any norm, such as Euclidean distance expressing the similarity between any observed data and the center of cluster [2].
uij=1 ŌłĆi=1,2,...,n, ŌłĆj=1,2,...,c), cj is the d-dimension center of the cluster, and ŌłźŌłź is any norm, such as Euclidean distance expressing the similarity between any observed data and the center of cluster [2].