A Selective Encryption Algorithm Based on AES for Medical Information
Article information
Abstract
Objectives
The transmission of medical information is currently a daily routine. Medical information needs efficient, robust and secure encryption modes, but cryptography is primarily a computationally intensive process. Towards this direction, we design a selective encryption scheme for critical data transmission.
Methods
We expand the advandced encrytion stanard (AES)-Rijndael with five criteria: the first is the compression of plain data, the second is the variable size of the block, the third is the selectable round, the fourth is the optimization of software implementation and the fifth is the selective function of the whole routine. We have tested our selective encryption scheme by C++ and it was compiled with Code::Blocks using a MinGW GCC compiler.
Results
The experimental results showed that our selective encryption scheme achieves a faster execution speed of encryption/decryption. In future work, we intend to use resource optimization to enhance the round operations, such as SubByte/InvSubByte, by exploiting similarities between encryption and decryption.
Conclusions
As encryption schemes become more widely used, the concept of hardware and software co-design is also a growing new area of interest.
I. Introduction
The amount of medical image transmission has increased rapidly on the internet. Tele-medicine and e-health especially, have a basic need of digital visual data (image, audio and video) transmission [1-4]. The security problem of the medical image transmission also increase. For example, the necessity of fast and secure diagnosis is vital in the medical world. Since several years, the protection of multimedia data is becoming very important. The protection of this multimedia data can be done with encryption or data hiding algorithms. To decrease the transmission time, the data compression is necessary. So far, some resolutions [5,6] have been proposed to combine image encryption and compression. Some others [7,8] give the performance analysis on conventional encryption methods such as data encryption standard (DES), 3DES, international data encryption algorithm (IDEA) and advandced encrytion stanard (AES), and some compression method such as Joint Photographic Experts Group (JPEG) and so on. AES, a block cipher as the new encryption standard, scrambles computation is performed on a fixed block size 128 bits with the key and round numbers. The core computation is iterated for many rounds, while the number of the rounds depends on the key size. Increasing the number of rounds applied, improves the resistance of the AES algorithm to cryptanalysis attacks.
In this paper, we propose a novel algorithm for medical information encryption based on AES-Rijndael. First, we present selector component on the input state, the key size and the number of rounds used to our algorithm to adopt many kinds of the platforms. Second, the raw image or plain-text can be compressed using Huffman algorithm [9] so as to reduce the image size of input as well as cutting AES-encryption time by more than half. And third, the time of coding implementing AES can be the least, using loop unrolling and merging methods in our algorithm improving AES algorithm.
II. Methods
1. AES
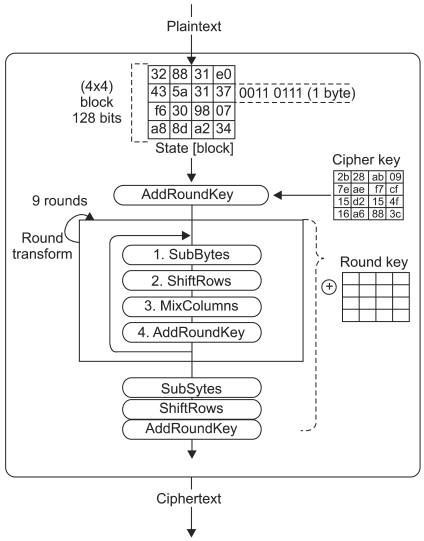
AES is an encryption standard adopted by the US government. The standard comprises symmetric block cipher AES from a larger collection originally published as Rijndael. Rijndael supports a range of block and key sizes; whereas the AES adopts a 128-bit block size and a key size of 128, 192 or 256 bits which has 10/12/14 rounds. In the AES-128 shown as Figure 1, a state is a 4 × 4 array of bytes, and the AES operates on states. The AES includes 10 rounds, where each round includes 4 stages except the last round. The 128-bit (16 byte) block is depicted as a square matrix of 4 × 4 bytes. The block is copied into the state array. This state array is modified at each stage of encryption or decryption and copied into the output array at the end. In each round of encryption and decryption, four operations are performed. They are: substitute bytes, shift rows, mixcolumns, and add round key. The mixcolumns operation is omitted in the last round and an initial key addition is performance before the first round for whitening.
The state array is subject to four operations in each round. The first one is substitution bytes transformations. In the SubBytes step, each byte in the array is updated using an 8-bit substitution box, the Rijndael S-box (16 × 16) shown as in Figure 2. This operation provides the non-linearity in the cipher. The S-box used is derived from the multiplicative inverse over GF (28), known to have good non-linearity properties. To avoid attacks based on simple algebraic properties, the S-box is constructed by combining the inverse function with an invertible affine transformation.
The ShiftRows step operates on the rows of the state; it cyclically shifts the bytes in each row by a certain offset shown in Figure 3. For AES, the first row is left unchanged. Each byte of the second row is shifted one to the left. Similarly, the third and fourth rows are shifted by offsets of two and three respectively.
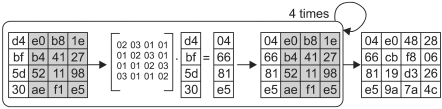
In the MixColumns step, the four bytes of each column of the state are combined using an invertible linear transformation. The MixColumns function takes four bytes as input and outputs four bytes, where each input byte affects all four output bytes. Together with ShiftRows, MixColumns provides diffusion in the cipher. In Figure 4, each column is treated as a polynomial over GF (28) and is then multiplied modulo x4 + 1 with a fixed polynomial c(x) = 03x3 + 02x2 + 01x + 01.
In the AddRoundKey step shown as Figure 5, the subkey is combined with the state. For each round, a subkey is derived from the main key using Rijndael's key schedule; each subkey is the same size as the state. The subkey is added by combining each byte of the state with the corresponding byte of the subkey using bitwise XOR.
The key expansion algorithm, the 128-bit key is taken as a square matrix of bytes. The AES key encryption algorithm takes a 4-word key as input and gives a liner array of nb(nr + 1) words. The nb is 4 (word key) and nr is the number of rounds where nr is 11 for AES-128, the key of which is then expanded into array of 44 key scheduled words asw[i] where 0 ≤ i ≤ nb(nr + 1). Initially the 4 word key is copied into the first four words of the expanded key. Then the remainder of the expanded key is filled in four words at a time. Each word is obtained by XORing the values of immediately preceding word and the word four positions back. In case of the position which is a multiple of 4, function Rot-word and function Subword are used, where the Rot-word performs a one-byte circular left shift on a word, and Sub-word is used to have a byte substitution on each byte of its input word using the S-box. The above two sub functions' results are XORed with a round constant. Round constant as Rcon[j], where 0 ≤ j ≤ 9, is a word in which three rightmost bytes are 0 so that the effect of an XOR with Round constant is performed on only the leftmost byte of the word. There is an example of the key expansion algorithm of AES-128 shown in Figure 6.
2. The Selective Encryption Algorithm (SEA)
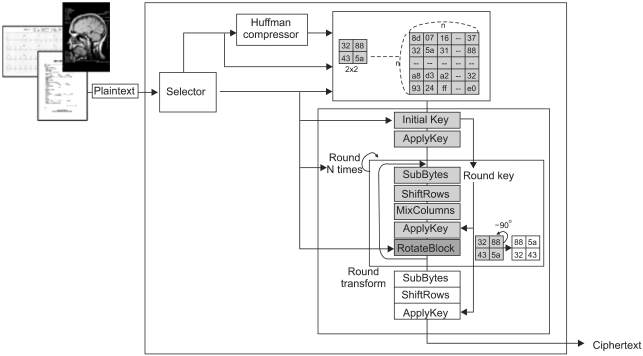
AES-Rijndael with 128/192/256 bit keys and 16 byte data treats data in 4 groups of 4 bytes, operating an entire block in every round. At that time, AES are considered not suitable for visual data such as digital image because of long computation process. Recent advances in hardware capability and improvement in software have led to achieve the optimal execution rate when we can find the size of input state by implementing our SEA algorithm system. The result shows that the size of input state among 20 × 20 to 30 × 30 can get the least execution time. In this paper, we proposed a novel encryption algorithm called SEA which is selective and improves the AES algorithm. The Architecture of SEA is shown in Figure 7. The Architecture allows one to perform core idea of our algorithm is a optional manner implemented by Selector component given in Figure 7. Since the current trend of medical image transmission over the network is more and more increasing. The digital visual data have some different types, like video, audio, Image, text file, and so on. As we known, many kinds of platforms from many kinds of devices are over the wire/wireless network. Therefore the selector component performs the selector function, where compression of the raw image or plain text noted as Cyn, the size of input state noted as InpS, the size of key noted as KeS and the number of round noted as Rn are optional and can be decided.
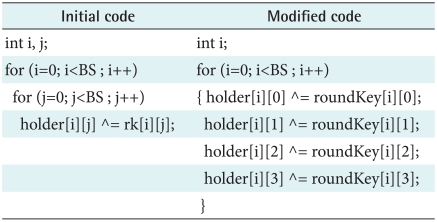
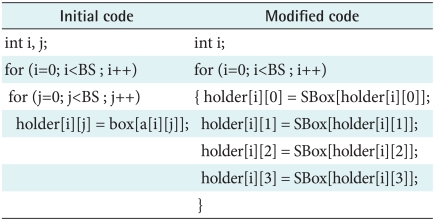
Recall that the resistance of AES-based encryption against cryptanalysis attacks depends entirely on the Rn used. The compression component using Huffman coding is proposed in our algorithm so as to reduce the Rn entirely used as well as keeping less implementation time. In the same breath, using compressed data as input state improves the resistance of AES against breaking attacks. The Huffman compressor component is shown in our algorithm architecture. The state-rotation function, a linear function lets input state do negative rotation by 90 degrees can be optional to add in our algorithm. Since many double circulation codes exist in the raw AES algorithm, it costs much time during it's implementation state. Therefore, our proposed algorithm performs unrolling and merging methods replacing the double circulation codes to keep its least implementation time, shown in Tables 1-3 [10].
III. Results
We study the performance of our algorithm on the platform as follows: Intel 2.4 GHz CPU and 2 GB RAM. A visual programming using c++ codes which have been made as Code::Blocks ver. 8.02 (The Code::Blocks team, free and open source) and then complied by MinGW GCC, has been used for implementing our algorithm. we compared our algorithm before compression to after compression on three kinds of input file like simple text (eg, english text file), complex text (eg, report, paper file) and Image file (eg, X-ray, CT, etc), given in Table 4.
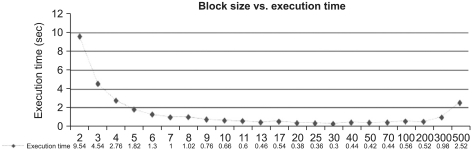
In order to make decision on three elements (InpS, KeS, Rn) which affects in our algorithm. The raw file and compressed file can be input state respectively and we compare the execution time of them. The throughput, say Tp, BlockSize meaning the size of input state and Clockcycle, a static variable of system hardware, can be expressed in terms of the round number, say Rn, is as in (1) can be found in [11]. The chart of Figure 8 show that the optimal situation arises when Blocksize is 30Code::Blocks ver. 8.0230.

Since pinpoint difference of execution time exists when Blocksize is around in [20 × 20 - 30 × 30]. we have used 160 bits key, input state 20 × 20 and 20 rounds in our proposed algorithm. Figures 9-11 show the results of algorithm execution time between two separate input data (raw data and compressed data) respectively. For the simple text, The execution time in encryption/decryption can be reduced more than 50% using our algorithm. In the mean time, the execution time in encryption/decryption can be reduced 25% for complex file and 40% for image file respectively.
IV. Discussion
In this paper, we have presented a selective encryption algorithm based on AES for medical information. We performed selector component on the input state, the key size and the number of rounds used to our algorithm adopted many kinds of platforms. And compressed image as input data not only gets high security and reduce much more than 35% of average execution time. The results show that our algorithm is more efficient and fast improving original AES algorithm. In future work, we emphasis on resource optimization to enhance the round operations, such as SubByte/InvSubByte, by exploiting similarities between encryption and decryption. As the encryption scheme becomes more widely used, the concept of hardware and software codesign is also a growing new area of interest.
Notes
No potential conflict of interest relevant to this article was reported.